Cambio de rpm y rps a rad/d. How to convert radians per second to revolutions per second [rad/s to RPS]:. f RPS = 0.1591549433 × f rad/s. How many revolutions per second in a radian per second: If f rad/s = 1 then f RPS = 0.1591549433 × 1 = 0.1591549433 RPS. How many revolutions per second in 64 radians per second: If f rad/s = 64 then f RPS = 0.1591549433 × 64 = 10.1859163712 RPS

CONVERTIR RPM a RAD/S rpm a radianes por segundo rad/s a rpm y rev/min (fórmula ejercicios

Maestría Historiador convertir de rpm a radianes por segundo salir Entrada recoger

Cambio de unidades. De rpm a rad/s y de rad/s a rpm. YouTube

Conversão Rpm Para Rad/s ENSINO
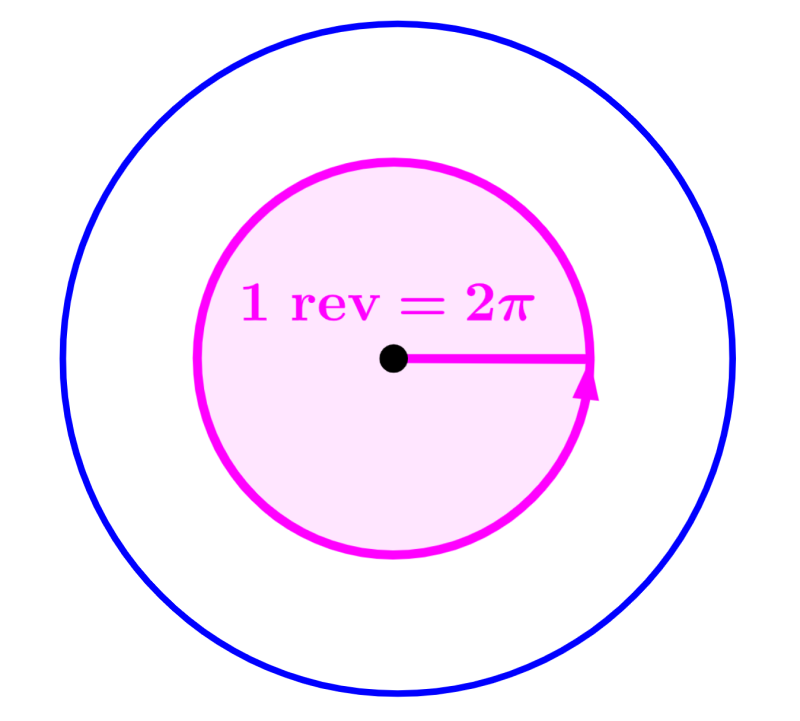
Convertir Revoluciones a Radianes Neurochispas

Convertir rad/s a rpm YouTube

Convert RPM to Rad/s Formula & Rad/s to RPM Converter Education quotes, Radians, Rad

Converting RPM to Radians Per Second Calculator How to Convert RPM to RPS?

CONVERTIR 5 REVOLUCIONES A GRADOS Y RADIANES YouTube

CONVERSIÓN DE UNIDADES r.p.m. a rad/s r.p.s. a rad/s MCU PARTE 3 EN VIVO YouTube

¿Cuantas (r.p.m) son 4 rad/s?? formula para calcularlo? Brainly.lat

Guia mcu 1 para página

Convertir RPS a Rad/s YouTube

CPM Precalculus 1132 Revolutions per minute to radians per second YouTube

Convert Radians per Second to Revolutions per Minute (Rad/S to RPM)

Convertir de GRADOS a RADIANES Explicación + Ejemplos YouTube

Convert RPM to Rad/s Formula & Rad/s to RPM Converter Education quotes, Converter, Rad

Cambio unidades rpm y rps a rad/s YouTube
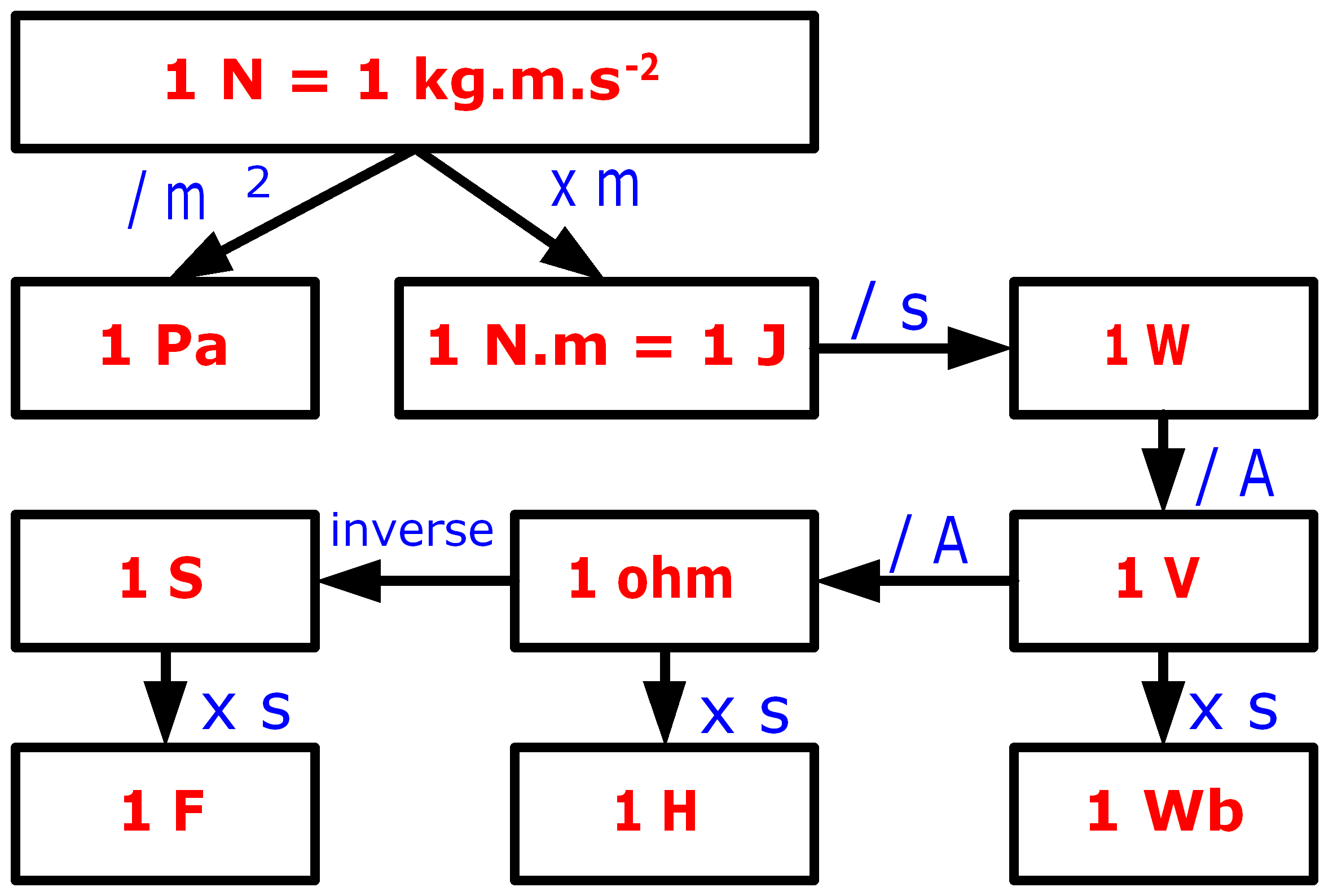
EXERCICE Convertir dans l`unité indiquée a) 1,2 m3 en dm3 9,4

velocidad angular rpm a rad/s
To convert RPM to angular speed in rad/s, multiply the RPM value by 2π/60. How to convert 60 RPM to RPS? To convert 60 RPM (Revolutions per Minute) to RPS (Revolutions per Second), divide 60 RPM by 60: 60 RPM / 60 = 1 RPS. What is 200 rad/s in RPM? 200 rad/s is equivalent to approximately 1909.86 RPM.. $$ \omega_{ (rad.s^{-1}) } = 2\pi.N_{(rps)} $$ This also means that the wheel rotates from \( \omega \) radians during one second. During that same second, the attached object (or point) travels a distance of \(r \times \omega \). It implies that the speed of the object is also equal to \(r \times \omega \). The conversion can be done thanks to.