Country: Spain. School subject: Matemáticas (1061956) Main content: Características de las funciones (1985039) Cálculo del dominio y el recorrido de una función a partir de su gráfica.. © http://selectividad.intergranada.com 3 Dominio de Definición Departamento de Matemáticas http://selectividad.intergranada.com © Raúl González Medina

Funcion lineal grafica dominio y rango Como graficar una funcion
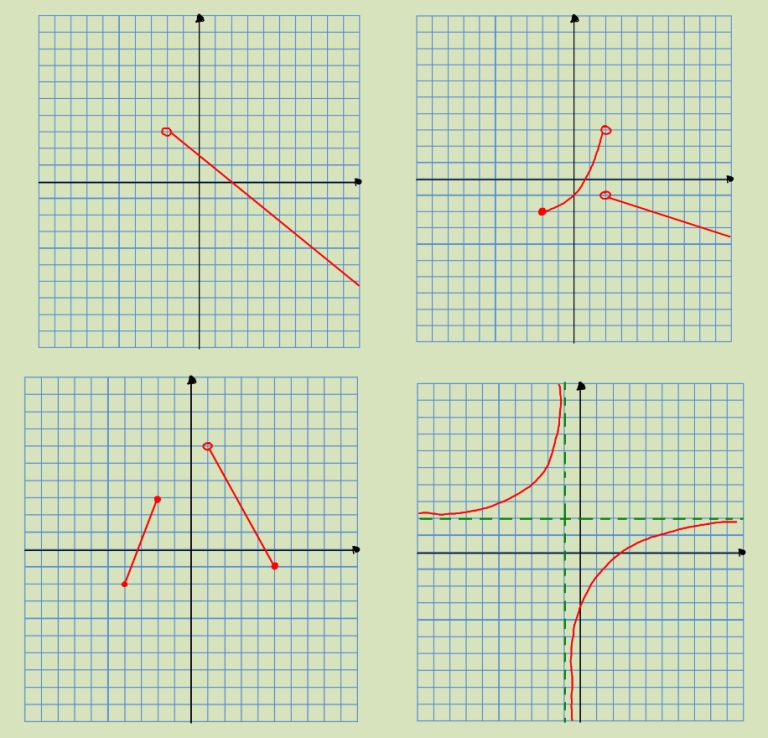
DOMINIO y RECORRIDO de una función a partir de su gráfica
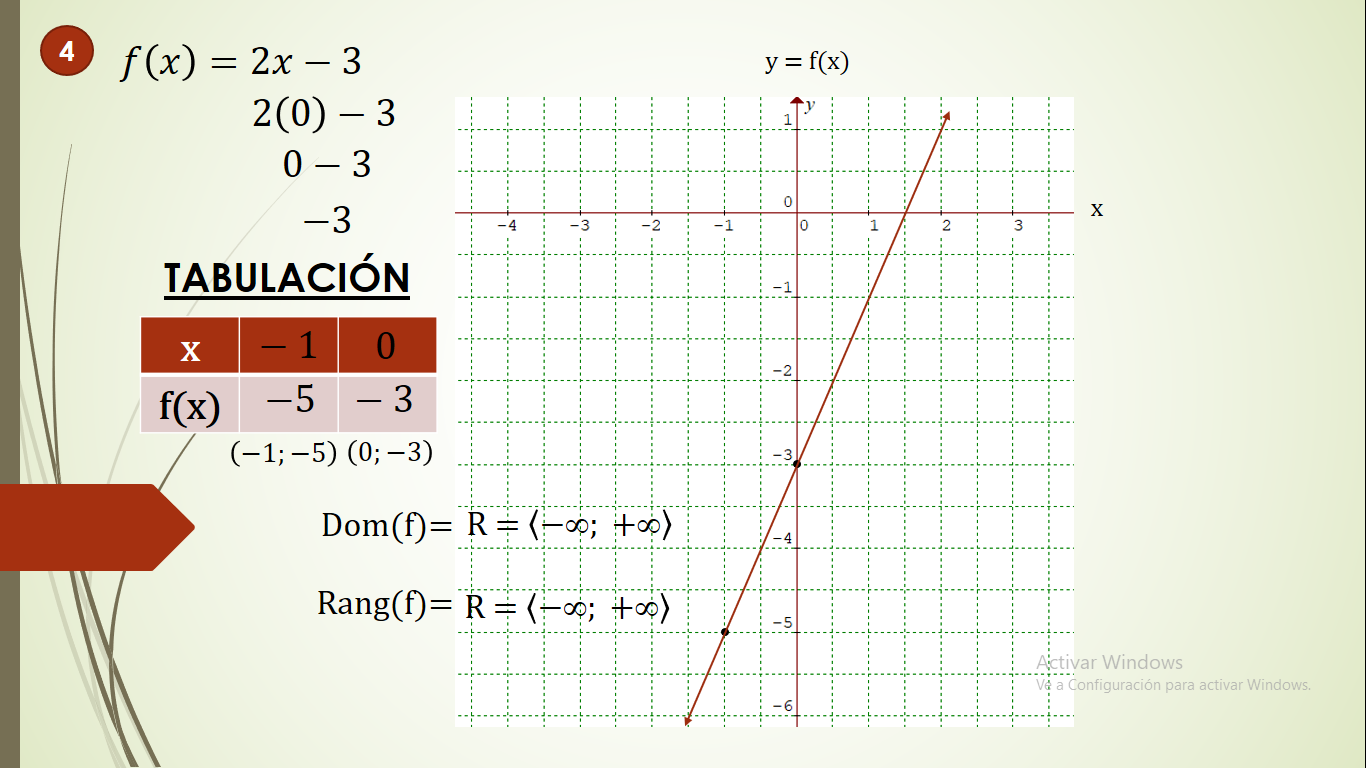
FUNCIONES LINEALES GRÁFICA DOMINIO Y RANGO
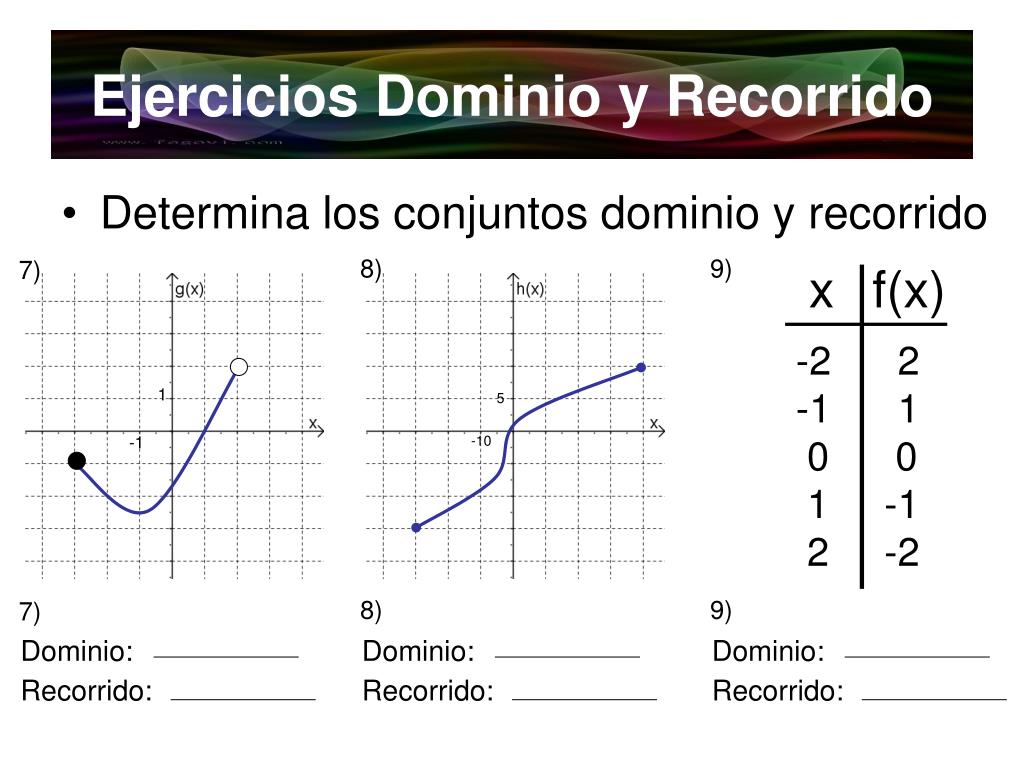
PPT DOMINIO Y RECORRIDO DE UNA FUNCIÓN PowerPoint Presentation, free
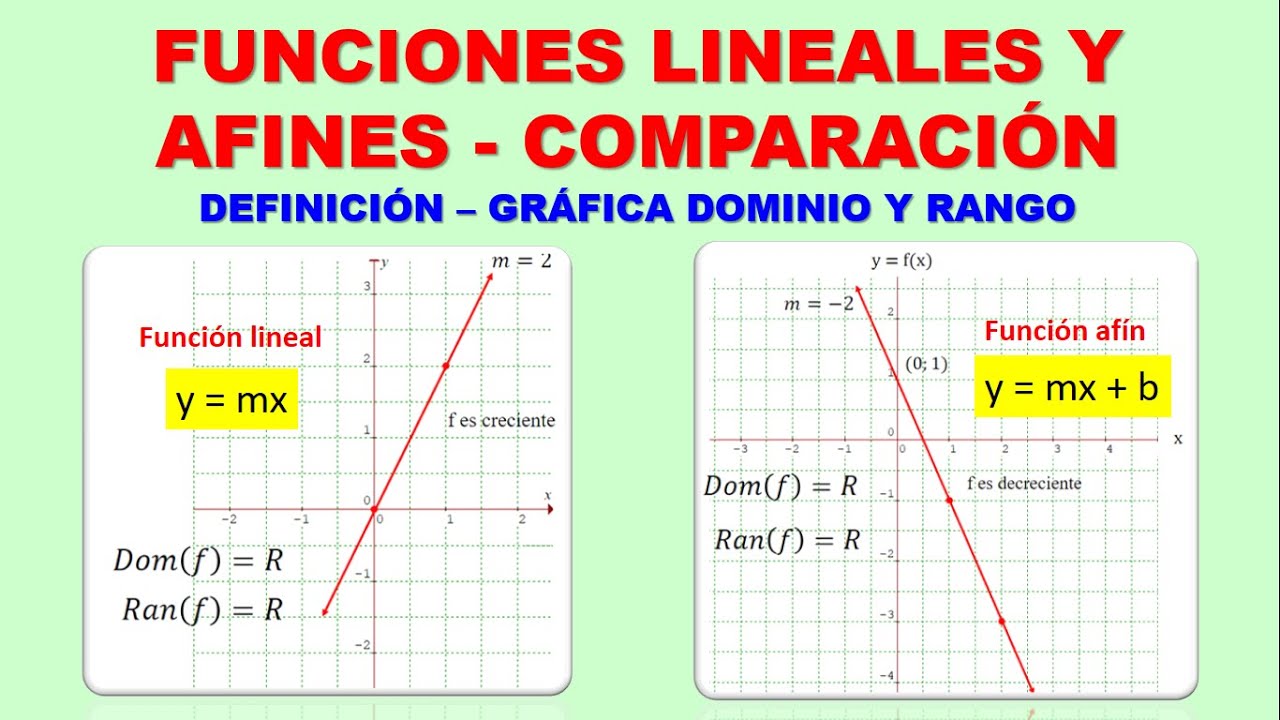
Funciones lineales y afines representación gráfica dominio rango y

FUNCIONES CUADRATICAS GRÁFICA DOMINIO RANGO 4 EJERCICIOS RESUELTOS

EJERCICIO ESTUDIO DE DOMINIO, RECORRIDO Y DISCONTINUIDAD. YouTube

GRÁFICA DE RELACIONES DOMINIO Y RANGO (2) YouTube
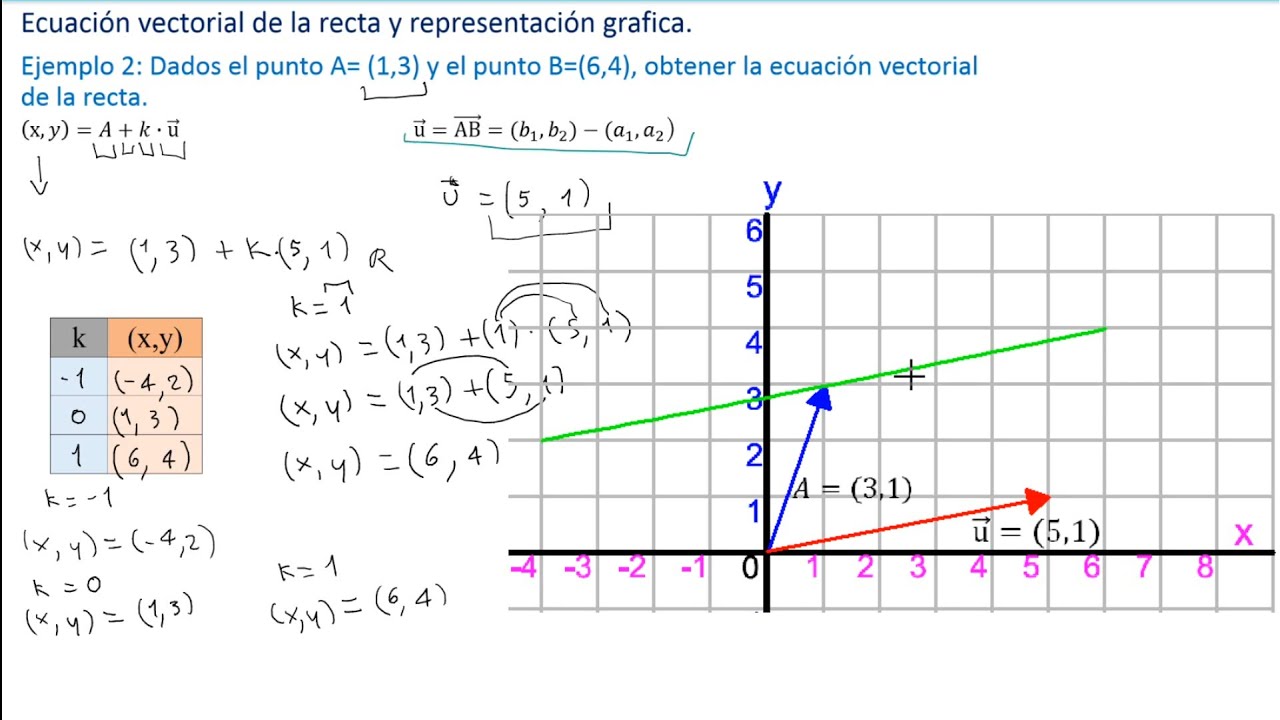
Ecuación vectorial de la recta, representación gráfica y ejercicios

Dominio y recorrido de una función Matemáticas 4ºESO YouTube

Dominio y recorrido de funciones polinómicas Mates Fáciles

FUNCIÓN VALOR ABSOLUTO (Ejercicio 2)/ DOMINIO/RANGO/GRÁFICA YouTube

Funciones Dominio y recorrido. 3º de ESO matemáticas YouTube
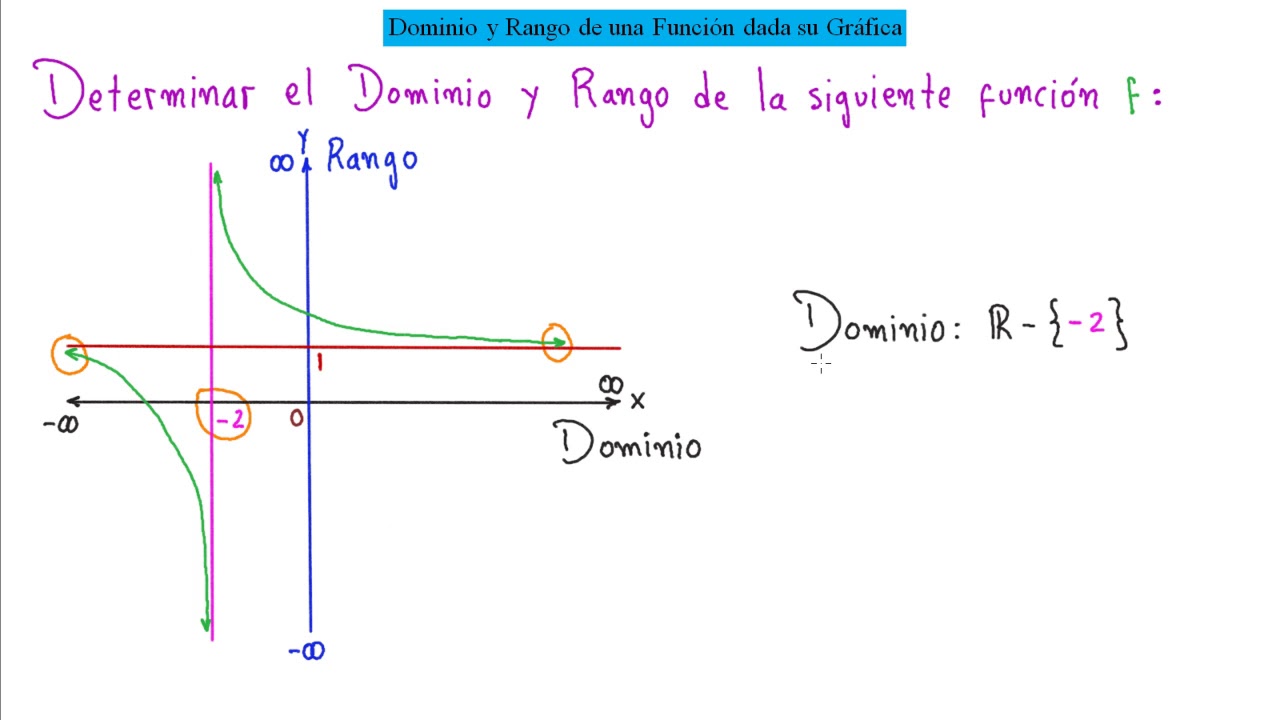
Aprende Rápido y Fácil a Obtener el Dominio y Rango de la Gráfica de

Dominio y recorrido de funciones racionales Mates Fáciles
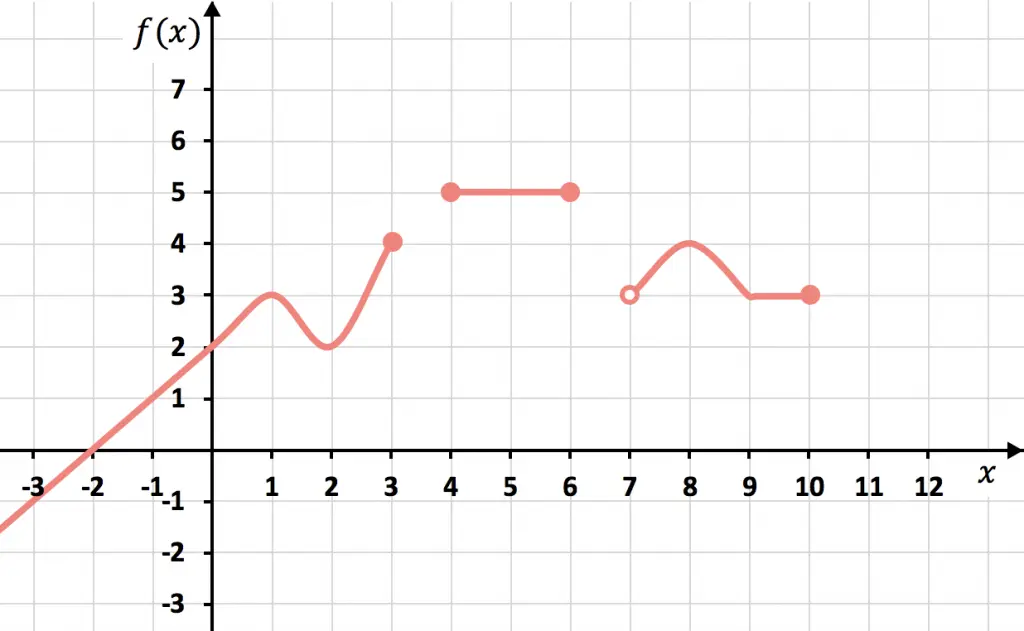
TODO sobre las Funciones (matemáticas) teoría, ejemplos,...
Solved Determina si es una función real, dada la tabla dee valores

Dominio y recorrido de una función YouTube

Funciones Dominio y recorrido. 3º de ESO matemáticas YouTube

Escribe el Dominio y Recorrido. Grafica la función 4 Ejercicios
4) Realiza un estudio completo de las siguientes funciones. a) b) a) Dominio : Dom f(x) = Q ( Todos los números racionales ) Recorrido : Rec f(x) = Q ( Todos los números racionales) La función es continua. La función es creciente : desde x = - ∞ hasta x = -1 y desde x = 1 hasta x = ∞ La función es decreciente: desde x = -1 hasta x = 1. Tiene un máximo relativo en el punto ( - 1, 2.. DOMINIO Y RECORRIDO. 1. DOMINIO. Dominio de f(x) o campo de existencia de f(x) es el conjunto de valores para los que está definida la función, es decir, el conjunto de valores que toma la variable independiente "x". Se denota por Dom(f). Dom ( f ) = { x ̨ ́ / $ y ̨ ́ con y = f ( x )}