Het eerste wat je zou kunnen zeggen en dit is een algemene manier om over dit soort oefeningen na te denken, is dat als ze jou een aantal graden geven en je moet weten hoeveel graden de anderen zijn dit altijd gebaseerd is op de totale hoeveelheid graden in een driehoek dat gelijkstaat tot 180, het kan ook zijn dat deze geen evenwijdige lijnen.. Je weet aan het einde van deze webpagina hoeveel graden een driehoek is. Je kunt aan het einde van deze webpagina hoeken berekenen doordat je weet hoeveel graden een driehoek is. Wat ga je doen? Je begin bij het kopje lesstof en daarna ga je naar het subkopje Voorkennis. Ga daarna naar het volgende kopje, de nieuwe subkopje(s) enzovoorts.

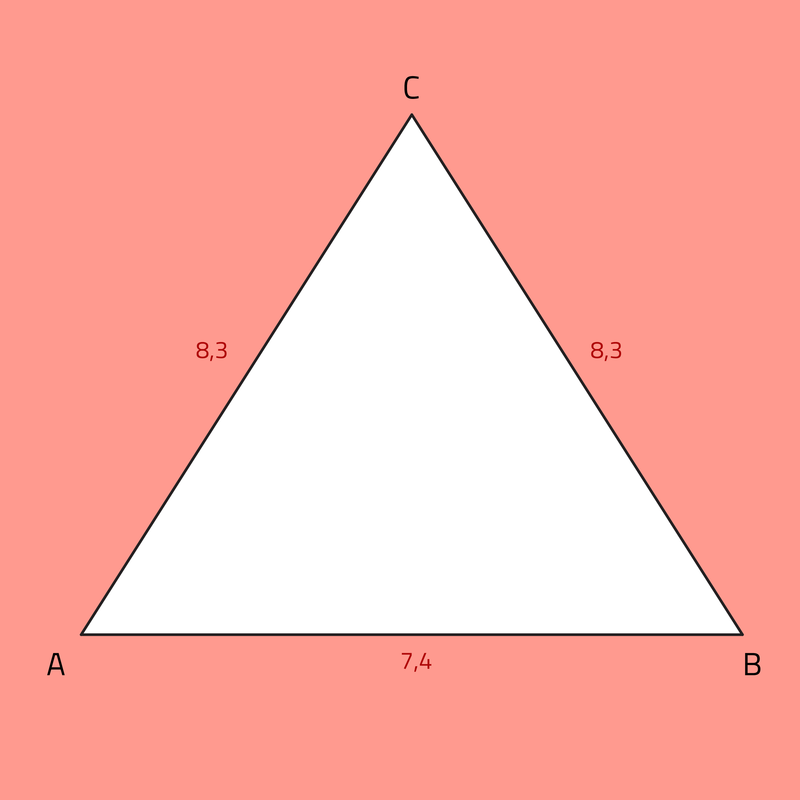
Slimleren Hoeken en zijden berekenen van gelijkbenige driehoeken

Wat Is Een Gelijkbenige Driehoek? Alles Wat Je Moet Weten! Chùa Phước Huệ

zijde berekenen van een rechthoekige driehoek YouTube

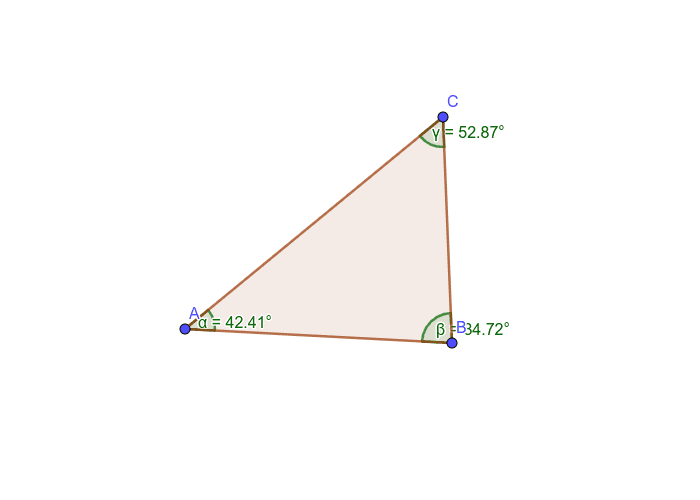
De hoeken van een driehoek GeoGebra

Driehoeken YouTube

Hoekensom van de driehoek YouTube

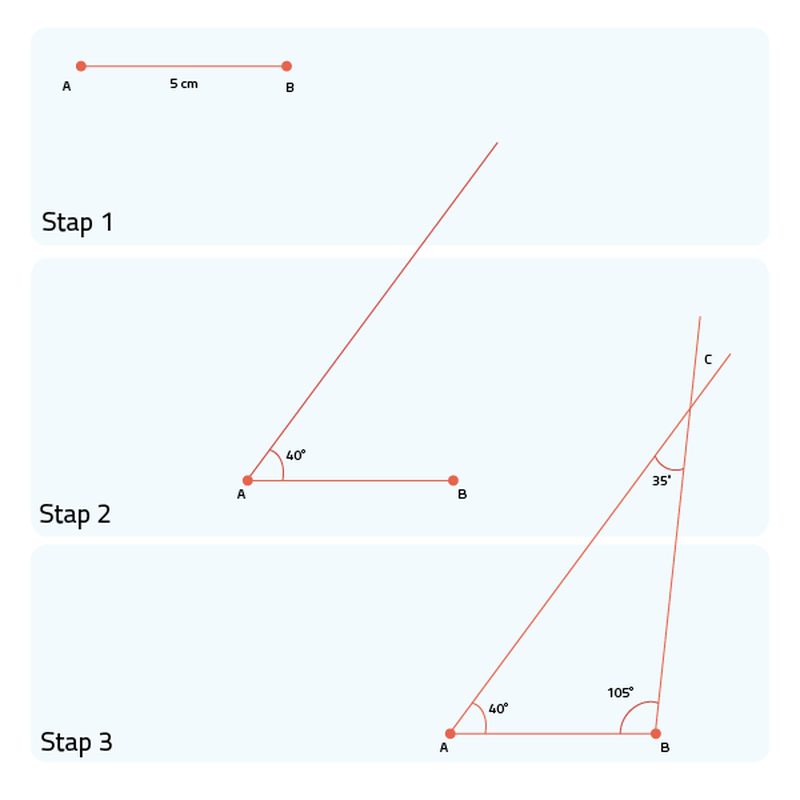
Slimleren Driehoeken tekenen

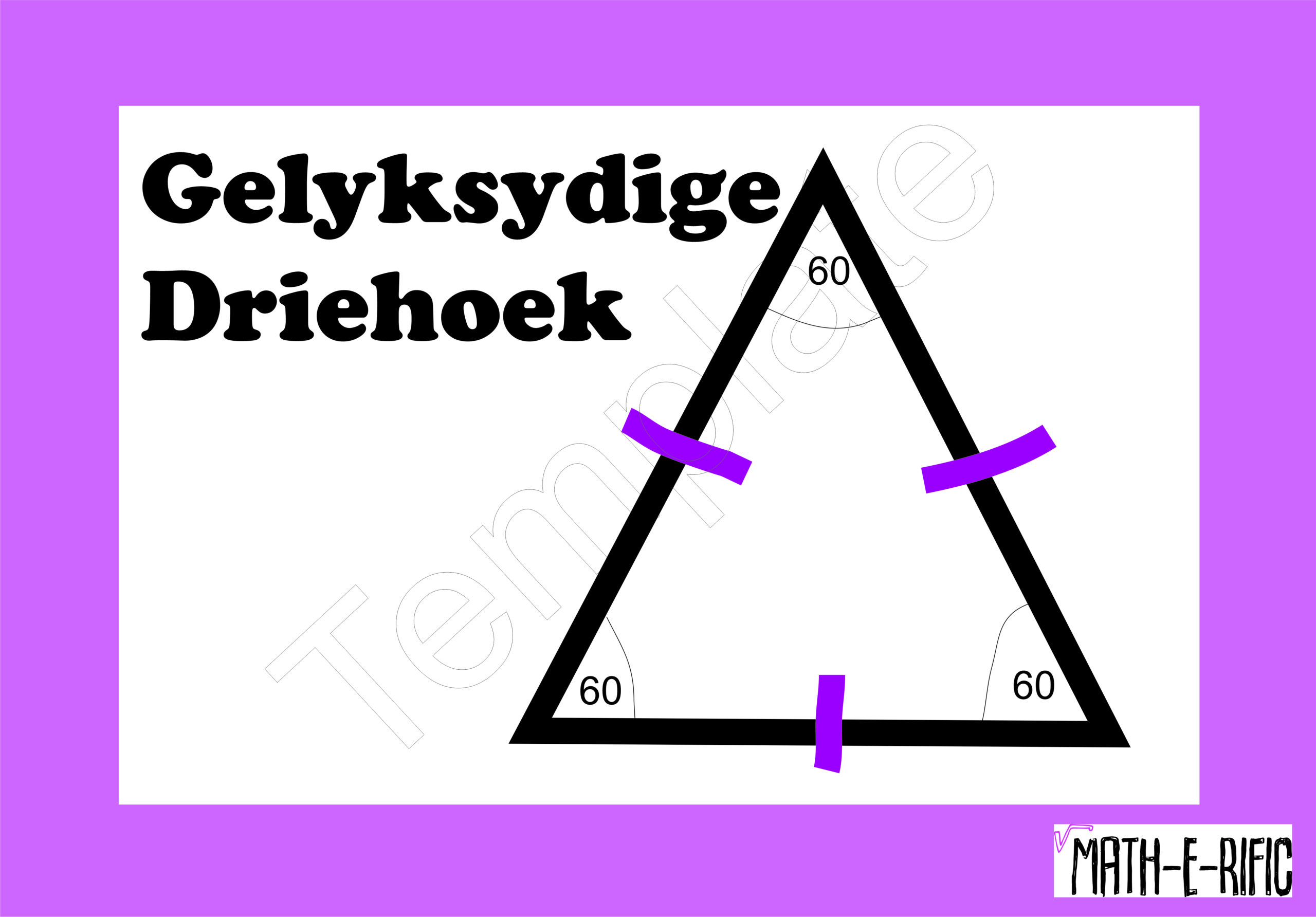
Tipe driehoeke 3 x A3 • Teacha!

Een driehoek tekenen met 3 gegeven zijden YouTube

Wiskunde bcenschede

Hoeken berekenen in figuren met meerdere driehoeken StudyGo

hoekensom driehoek YouTube

Goniometrie Gelijkbenige driehoeken (3 HAVO) YouTube

Wiskunde Hoekensom van een driehoek YouTube

Soorten driehoeken

Graden Berekenen

Graden Berekenen

Oppervlakte Driehoek

HoeDoeJe Een Gelijkbenige Driehoek Berekenen (Hoeken) YouTube

Voorbeeld hoek berekenen gelijkbenige driehoek YouTube

De oppervlakte van een driehoek wordt altijd berekend door: Oppervlakte = 1 2 × basis × hoogte (of basis × hoogte : 2) De basis is altijd één van de zijden van de driehoek. De hoogte is de (kortste) afstand van die zijde tot het tegenoverliggende punt. De hoogte en basis staan altijd loodrecht op elkaar.. Inleiding. Zoals je in het voortgezet onderwijs na een paar lessen wiskunde weet, is de som van de hoeken van een driehoek 180 graden. Dit artikel geeft een drietal bewijzen van deze eigenschap. In de vlakke meetkunde werken we met rechte lijnen, hoeken en cirkels. Een rechte lijn is de kortste verbinding tussen twee punten.