問題の一階線形微分方程式 \((1)\) の両辺に \(\mu\) をかけると、\((4)\) のような、積分するのに都合の良い形に変形することができました。 このように、微分方程式に掛け算して、それを積分して解ける形にするために使う関数を 積分因子 (integrating factor) と.. 【微分方程式の全リスト】https://youtube.com/playlist?list=PLvJgUfWjlUOVWVbZDFBXyfCRPyEPRbRV8一階線形微分方程式の解き方!例題付きです.

【大学数学解説】 ズルい! 楽単 解析学 微分方程式編 第3回 一階線形 Web塾 TAKING YouTube

一階微分方程積分因子 Budzak

『一階線形微分方程式』「公式使わず解いてみる。」(意欲的な高校生のための【大学数学】)जापानी गणित पहिलो क्रम रैखिक भिन्न समीकरण YouTube

1階線形常微分方程式|単位の密林

書記が数学やるだけ84 1階常微分方程式2(1次の同次形,1階線形微分方程式)|Writer_Rinka

一阶微分方程最全解法 简洁 常微分总结_哔哩哔哩 (゜゜)つロ 干杯bilibili

退職教授の見果てぬ夢 微分方程式講義(2016年版)IV
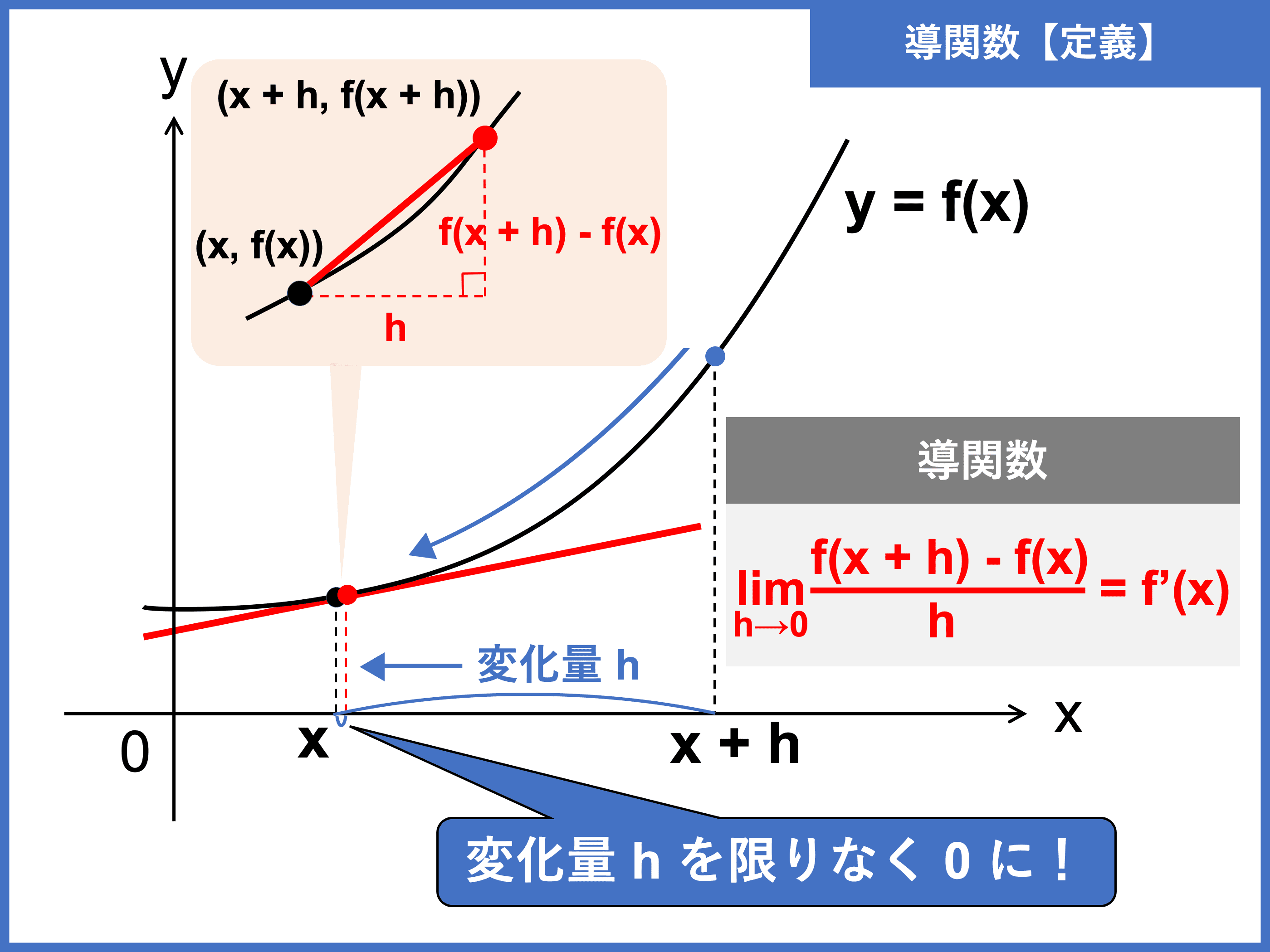
微分とは?微分のやり方と全公式をわかりやすく解説! 受験辞典

微分方程式6:斉次線形微分方程式その3 (減衰振動) YouTube

定数係数の一階同次連立線型微分方程式 たかくんの成長
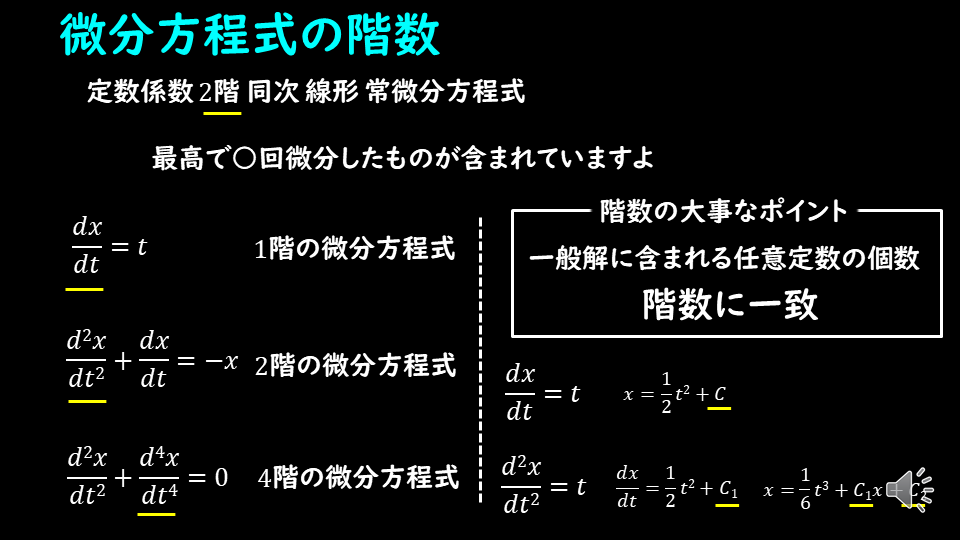
微分方程式の基礎④階数?同次?線形?常微分?名前の付け方を解説 デルタ先生の物理と数学の部屋

1階線型微分方程式の解き方 YouTube

微分方程式 星の本棚

微分方程式7:斉次線形微分方程式その4 YouTube

退職教授の見果てぬ夢 微分方程式講義(2015年版)II

y' + 5y = 6e^x【1階線形微分方程式】 YouTube
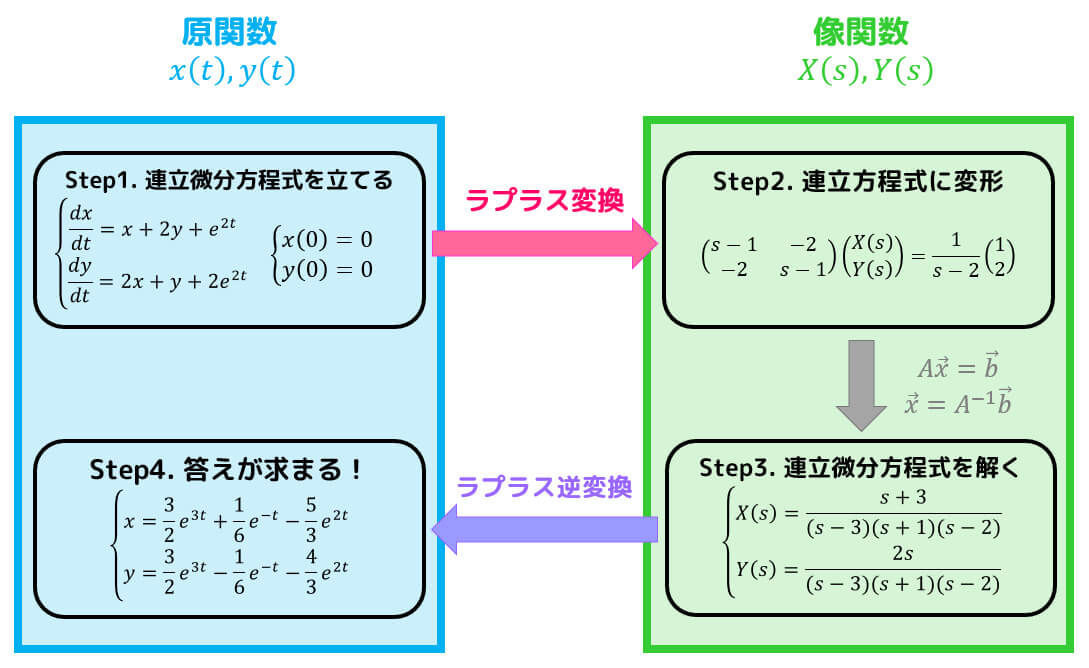
うさぎでもわかる微分方程式 Part15 ラプラス変換を用いた微分方程式・連立微分方程式の解き方 工業大学生ももやまのうさぎ塾

微分方程式5:斉次線形微分方程式その2 YouTube

常微分方程求通解时为什么不考虑x为0的情况? 知乎

常微分方程式 まとめ【更新2018/10/11】 たかくんの成長
すなわち,二階微分方程式の一般的な解法である定数変化法を一階微分方程式に当てはめるという対策は,数検1級においては推奨されないと考えています。 そこで,一階微分方程式特有の解法を身につける必要があります。これはそこまで難しくありません。. 一階常微分方程式 (first order ordinary differential equations) を解く基本的な方法を整理します。. 微分方程式の形によって、微分方程式の解法が異なります 。. つまり「ナントカ形の微分方程式のときは、こんな解き方で解ける!. 」というパターンがいくつかあり.