「線形」 と 「非線形」 の違いを、分かりやすく解説します。 「線形」 と 「非線形」 は、どちらも数学的な概念で使用される言葉ですが、それぞれ異なる特徴や用途を持ちます。. 特に制御工学の一分野として、線形システムを使ってその安定性や可制御性を調べる分野は、 線形システム論 と呼ばれています。一方、非線形システムを対象とする場合、非線形子システム論と呼ばれます。
線形計画法とは？例題（文章題）の解き方をわかりやすく解説！ 受験辞典
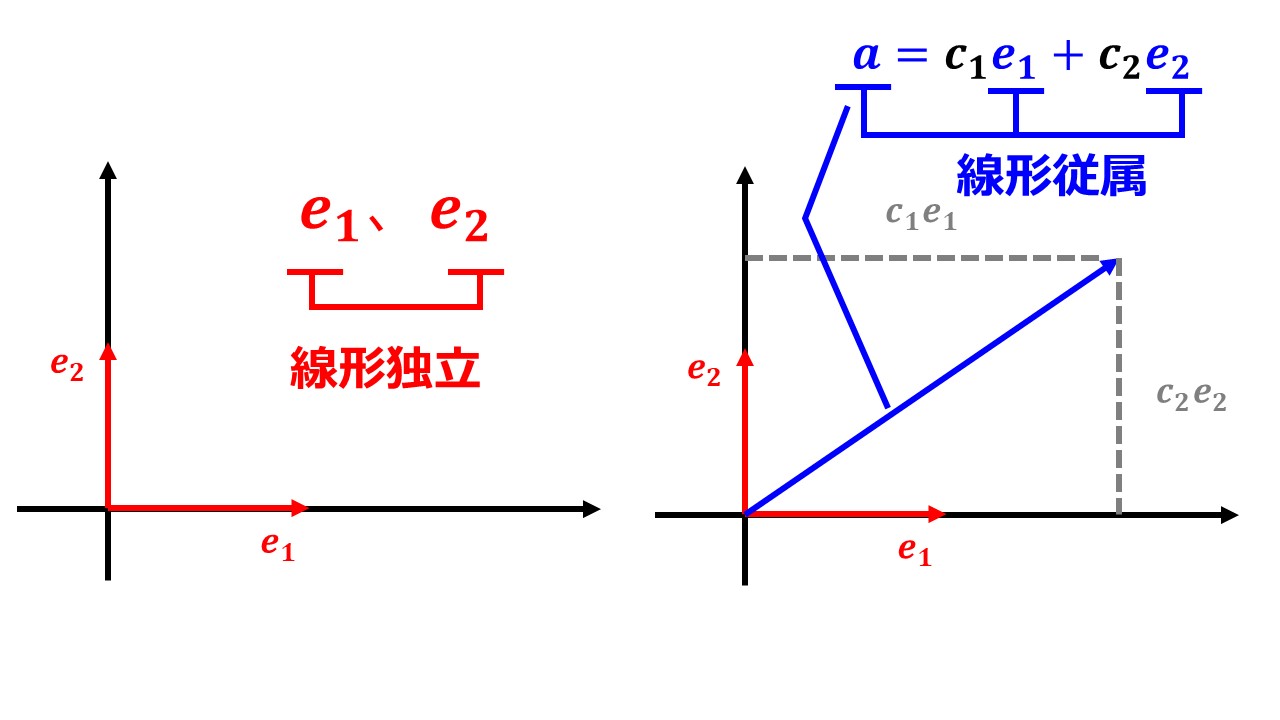
線形独立と線形従属をわかりやすく解説｜宇宙に入ったカマキリ
![Xの変数を適切に非線形変換して線形の回帰モデルを作るとモデルの適用範囲・適用領域が広がるかも！[検証結果とPythonプログラムあり] データ化学工学研究室(金子研究室)＠明治大学 理工](https://datachemeng.com/wp-content/uploads/SnapCrab_NoName_2018-7-28_10-29-30_No-00-768x773.png "Xの変数を適切に非線形変換して線形の回帰モデルを作るとモデルの適用範囲・適用領域が広がるかも！[検証結果とPythonプログラムあり] データ化学工学研究室(金子研究室)＠明治大学 理工")
Xの変数を適切に非線形変換して線形の回帰モデルを作るとモデルの適用範囲・適用領域が広がるかも！[検証結果とPythonプログラムあり] データ化学工学研究室(金子研究室)＠明治大学 理工
大学数学 微分方程式の線形と非線形の違いetc. YouTube
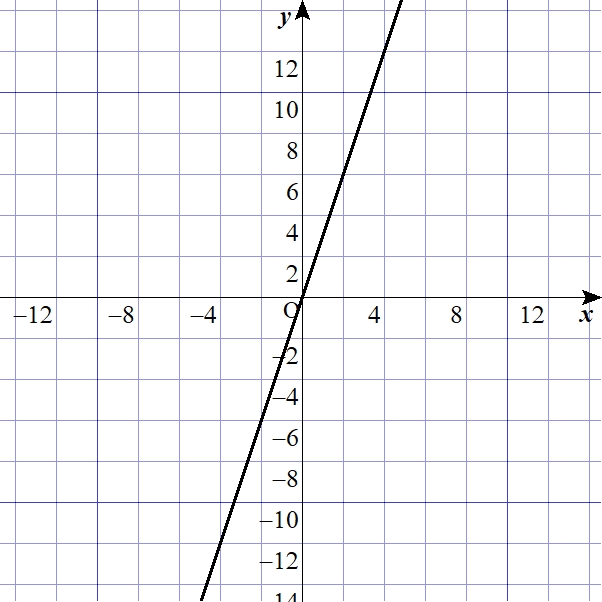
線形・非線形とは 「非線形」ってナンセンス？ 高井セミナー
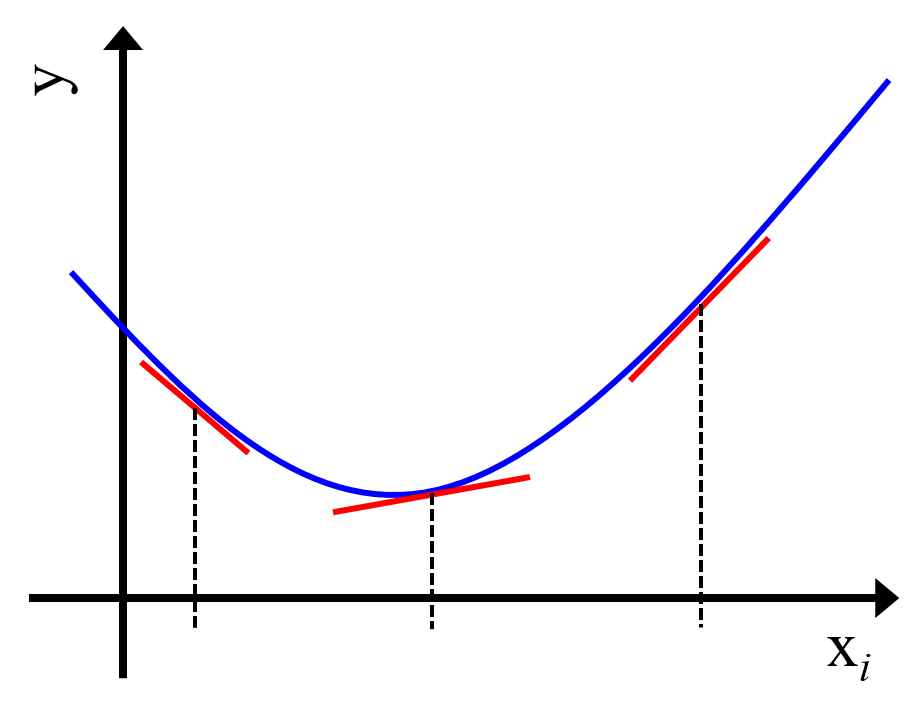
非線形モデルの解釈をしよう！～非線形モデルを各変数で偏微分～ データ化学工学研究室(金子研究室)＠明治大学 理工学部 応用化学科
非線形微分方程式【東大院試数学】 YouTube
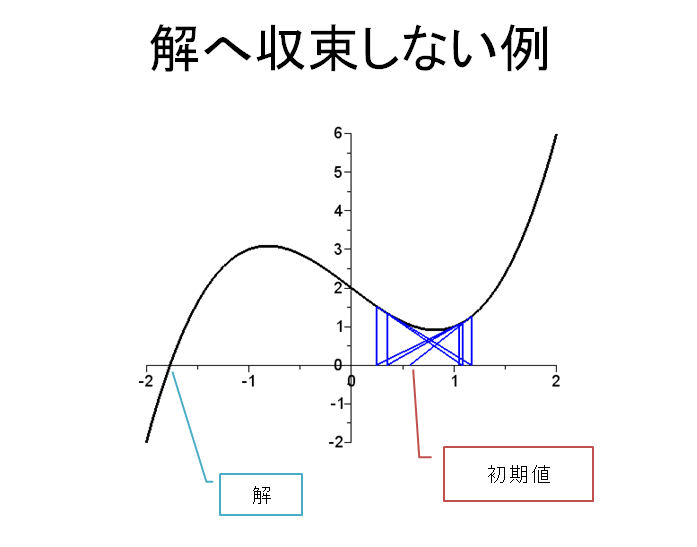
非線形方程式の数値解法
![[制御] 非線形システムの線形化 part 2 フィードバック線形化（1分でわかるシステム制御理論19） YouTube](https://i.ytimg.com/vi/9VC4bUYF058/maxresdefault.jpg "[制御] 非線形システムの線形化 part 2 フィードバック線形化（1分でわかるシステム制御理論19） YouTube")
[制御] 非線形システムの線形化 part 2 フィードバック線形化（1分でわかるシステム制御理論19） YouTube
線形解析と非線形解析の使い分け Altair Japan公式ブログ
【機械学習：Pythonコード有】線形と非線形モデルの違いと使い分け DSE総研オンライン｜データサイエンス教育総合研究所
線形解析と非線形解析の違い｜コラム｜株式会社ファソテック
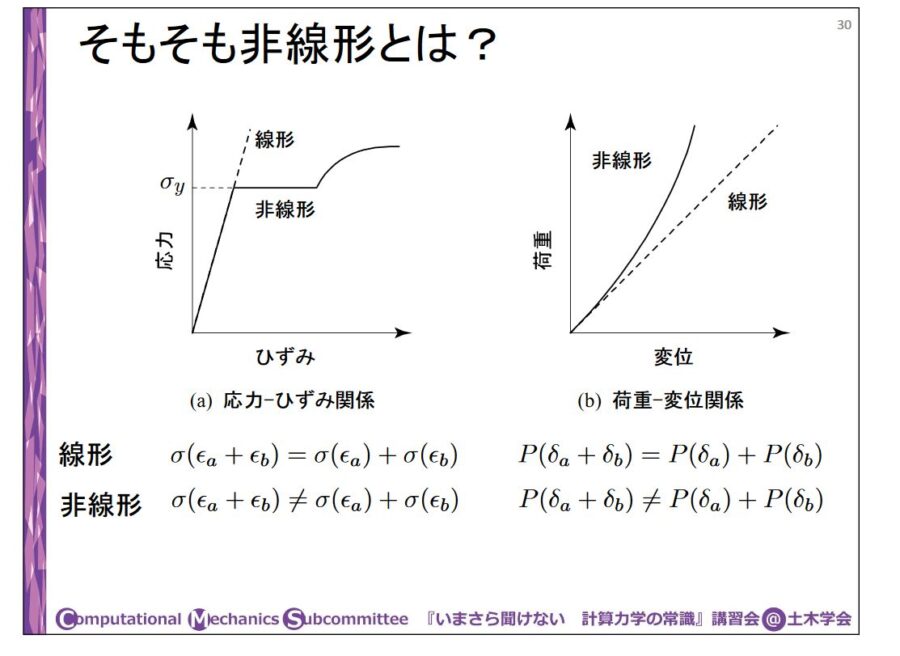
数学・科学における「線形・非線形」の違いを詳しく解説 趣味の大学数学
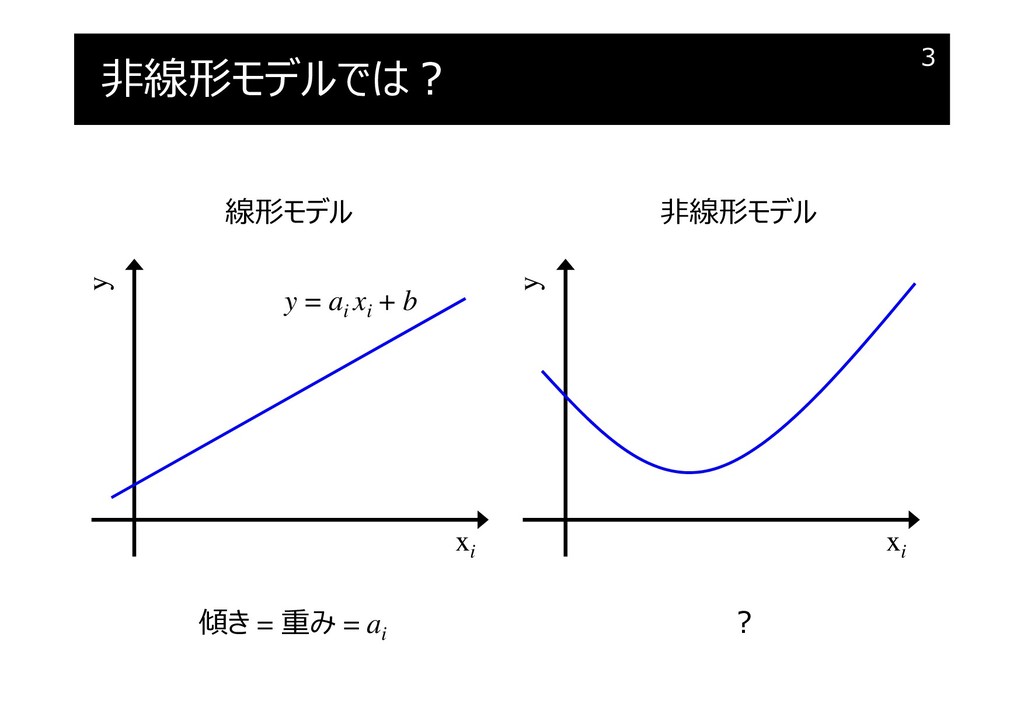
モデルの微分による非線形モデルの解釈 Speaker Deck
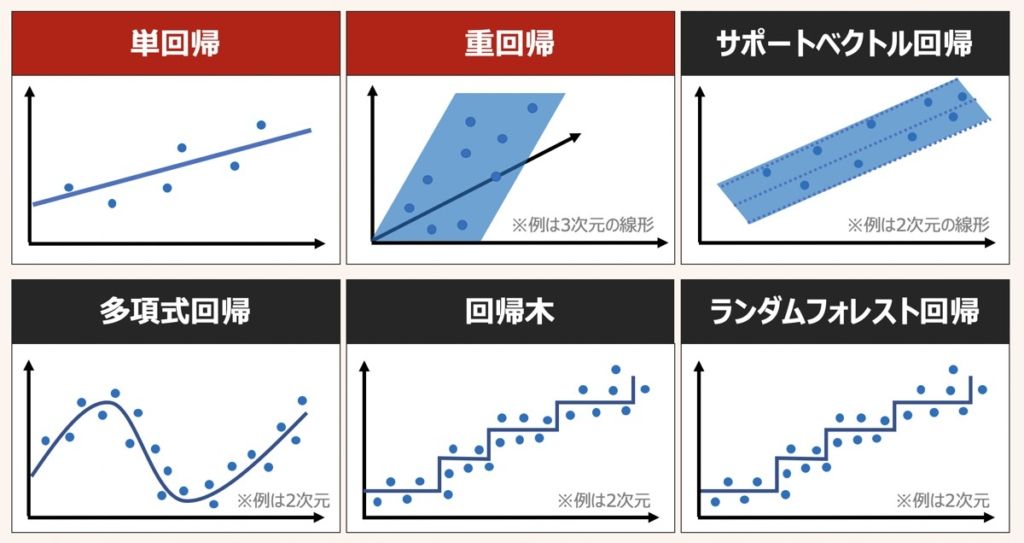
線形単回帰・重回帰分析とは？｜回帰モデル導出・評価における統計学的理論や機械学習への応用方法を分かりやすく解説
線形解析と非線形解析の違い｜コラム｜株式会社ファソテック
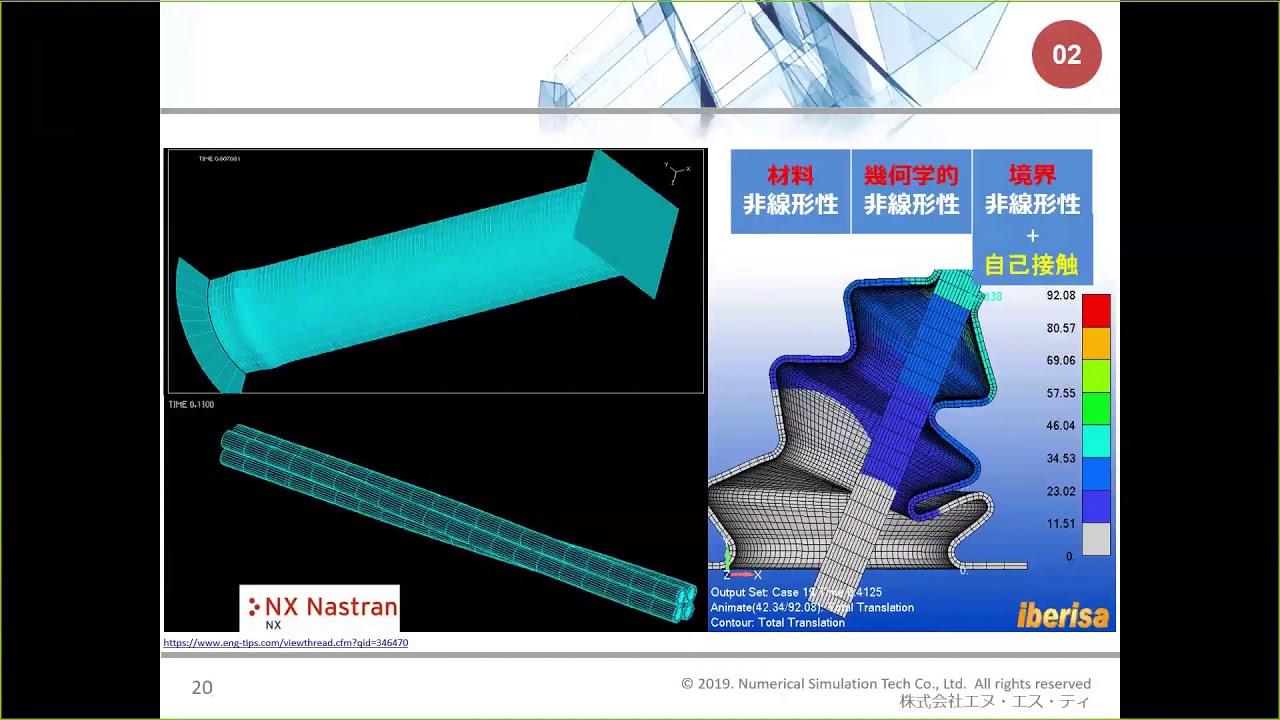
基礎からわかる非線形構造解析 第1回：非線形構造解析の概要 YouTube
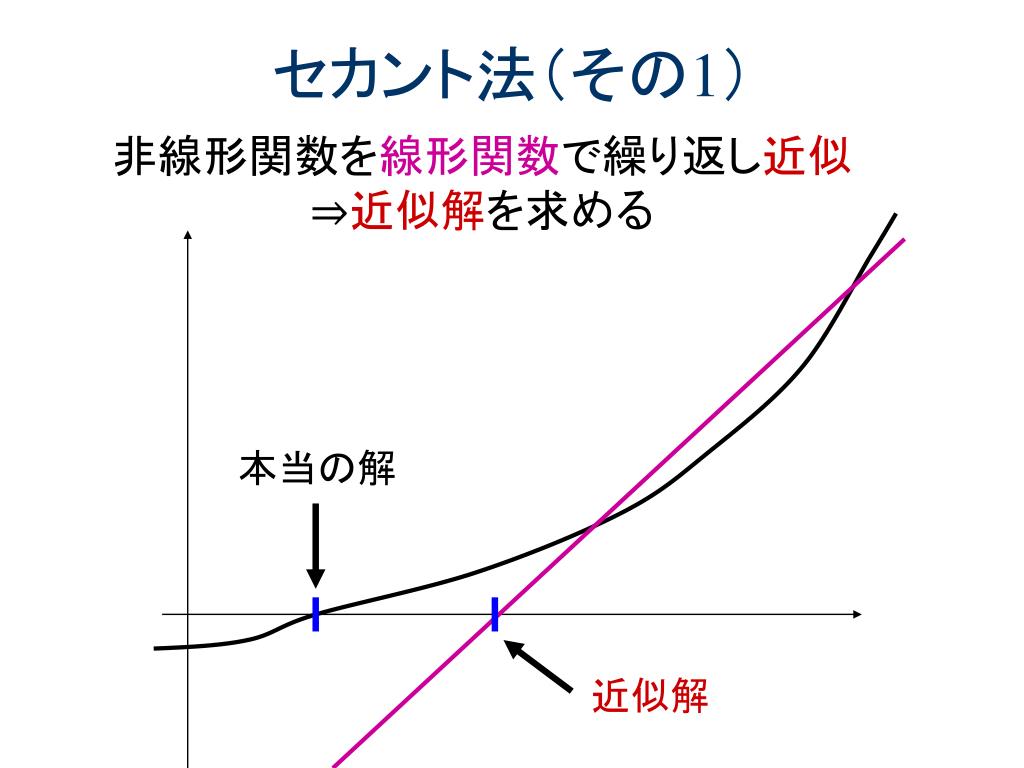
PPT 非線形方程式に対する 反復解法 （2回目） PowerPoint Presentation ID1009711
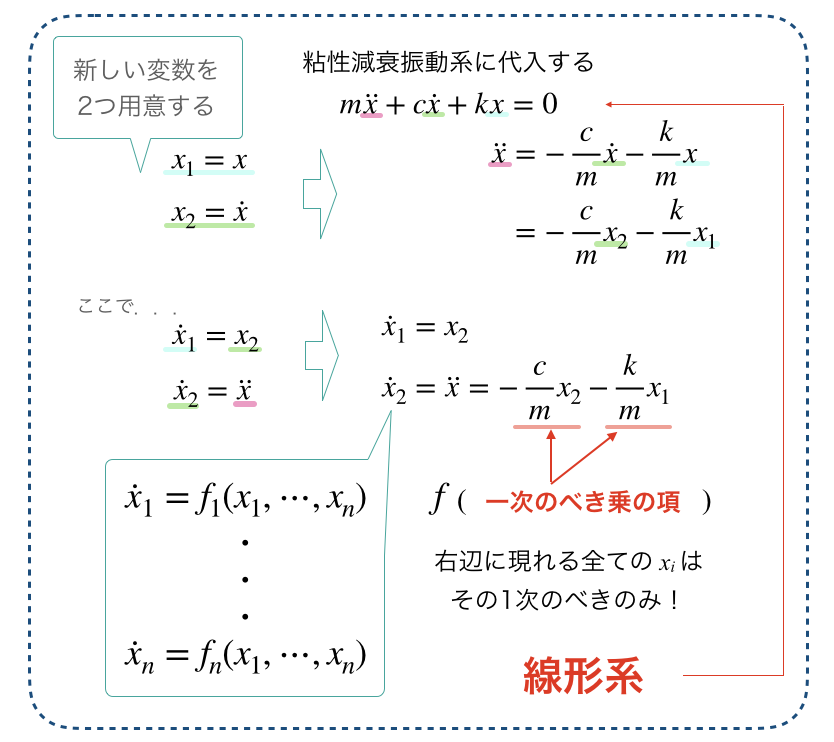
非線形微分方程式の解を幾何学的に算出する
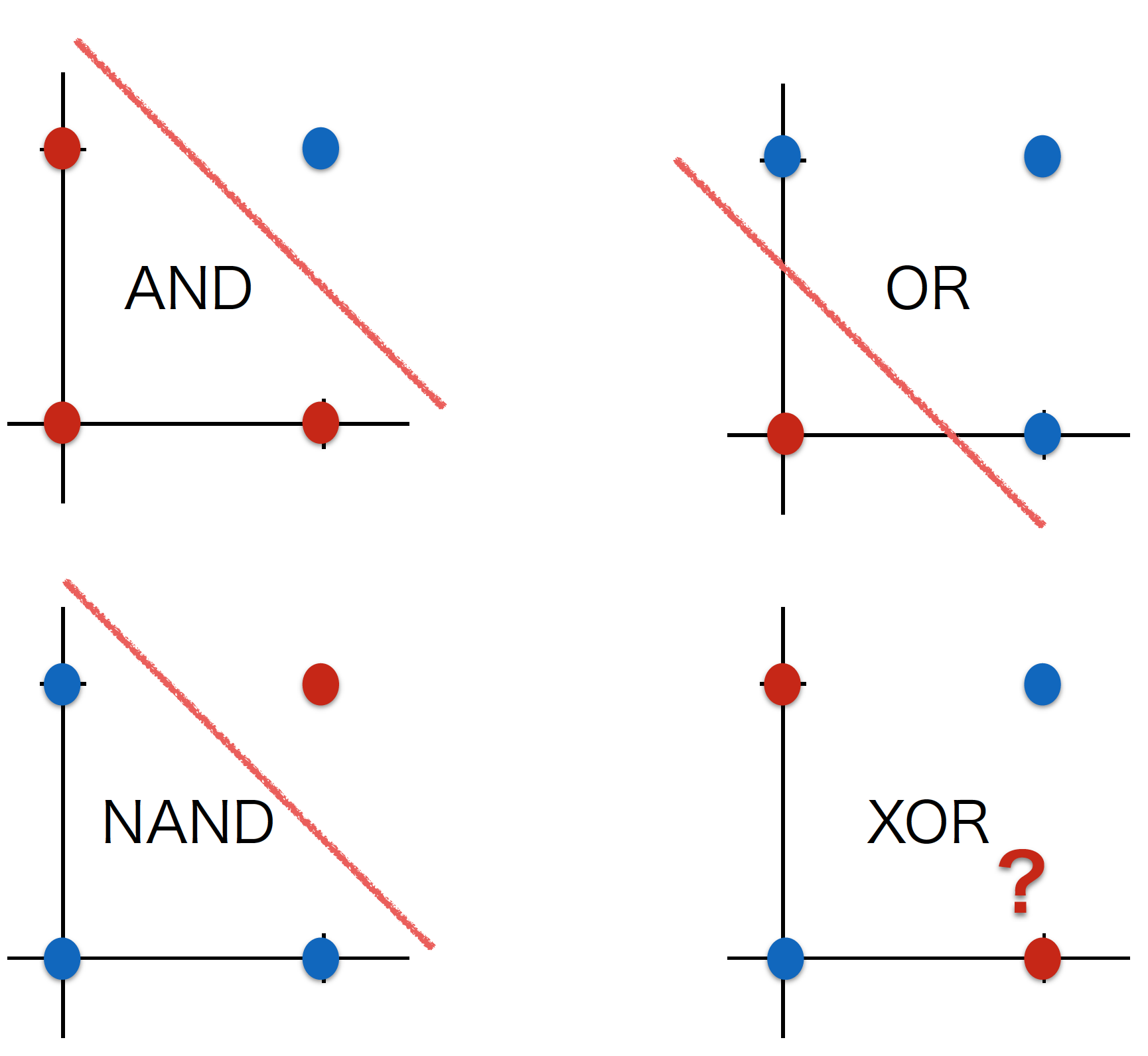
ニューラルネットワーク なぜDEEPにするのか？（非線形関数と線形関数） Qiita
線形代数とは 大学・高専の線形代数の全体像と流れ，参考書 線形性が見られる例 いわゆる「定数は外に出せる」と「項をそれぞれ演算すればよい」ということが見て取れます。. 非線形とは、力と変形、応力ひずみの関係が、比例関係にない状態です。比例関係にある状態を線形といいます。非線形の問題は、線形問題に比べて扱いにくく、高度な計算が必要です。今回は、非線形の意味と定義、線形との違い、非
